Вы находитесь на первом сайте биотической регуляции. С 14 февраля 2008 г. он не обновляется. Добро пожаловать на www.bioticregulation.ru! |
Актуальные исследования: Биотический насос атмосферной влаги
|
Комментарии и ответы |
Комментарий
Довгалюк Ю. (2006) Интерактивный комментарий к
статье "Биотический насос атмосферной влаги как движущая
сила круговорота воды на суше" А. М. Макарьевой, В. Г.
Горшкова. Гидрология и Науки о Системе Земля, Обсуждения,
3, S1135-S1137 (англ.)
www.cosis.net/copernicus/EGU/hessd/3/S1135/hessd-3-S1135.pdf
Внимание: русский перевод комментария Ю. Довгалюк выполнен В. Г. Горшковым и А. М. Макарьевой. Оригинальный английский текст представлен по указанному выше адресу. Я прочитала статью с большим интересом; авторы пытаются построить логически последовательную картину атмосферной циркуляции, базируясь на так называемой силе испарения, которую они вводят. Я должна признать, что не обнаружила ошибок в их изложении. Однако, пытаясь проанализировать утверждения авторов в рамках традиционных метеорологических принципов, я испытываю некоторое замешательство. Хотя авторы и затрагивают вопрос о том, как их новый физический подход соотносится с некоторыми базовыми метеорологическими понятиями (сс. 2637-2638), однако с моей точки зрения этот вопрос заслуживает гораздо более детального обсуждения. |
ОтветМакарьева А.М., Горшков В.Г. (2006) Интерактивный комментарий к статье "Биотический насос атмосферной влаги как движущая сила круговорота воды на суше" А. М. Макарьевой, В. Г. Горшкова. Гидрология и Науки о Системе Земля, Обсуждения, 3, S1176-S1184. www.cosis.net/copernicus/EGU/hessd/3/S1176/hessd-3-S1176.pdf Внимание: русский перевод комментария выполнен авторами. Оригинальный английский текст представлен по указанному выше адресу. В ответ на комментарии Ю. Довгалюк: Др. Довгалюк ставит вопрос о том, как понятие биотического насоса и его физический механизм (сила испарения) соотносятся с общепринятыми парадигмами современной метеорологии, а именно (1) с понятием конвективной неустойчивости для вертикальных движений воздуха и (2) температурно-обусловленным барометрическим градиентом для горизонтальных движений воздуха. В нашем ответе мы вначале покажем, как предложенный нами подход позволяет количественно описать основные наблюдаемые параметры атмосферной циркуляции, а затем обсудим преимущества предложенного подхода и критические положения в традиционной метеорологической парадигме. | |
|
1. В метеорологии потоки явного тепла связываются с конвективной неустойчивостью воздушных масс; эта неустойчивость возникает в условиях наблюдаемого отрицательного вертикального градиента Gob = 6.5 К/км. Если случайно образуется ограниченный объем воздуха с положительной плавучестью, т.е. более нагретый и, следовательно, более легкий, чем равные объемы окружающей атмосферы, то такой объем под воздействием архимедовой силы начнет подниматься вверх. Как хорошо известно, при адиабатическом подъеме происходит охлаждение со скоростью 9.8 К/км для сухого воздуха и около 6 К/км для влажного атмосферного воздуха при сохранении сконденсировавшейся влаги внутри поднимающегося объема. Так как наблюдаемое охлаждение атмосферы с высотой, равное 6.5 К/км, больше по абсолютной величине адиабатического охлаждения влажного воздуха, то поднимающийся объем воздуха остается теплее и легче равных объемов окружающей среды и, следовательно, будет неограниченно долго подниматься в атмосфере. Соответственно, объемы с первоначальной большей плотностью (отрицательной плавучестью) будут неограниченно долго опускаться вплоть до земной поверхности. Подъем и опускание этих случайно возникающих масс воздуха создают турбулентные потоки, из которых и складываются потоки скрытого и явного тепла. Потоки явного и скрытого тепла равномерно перемешивают тропосферу, что приводит к одинаковому распределению по высоте всех парциальных газов, составляющих воздух. Эти же турбулентные потоки поддерживают облачность на фиксированных высотах в тропосфере. 2. В метеорологии полагается, что в условиях турбулентного перемешивания влажного воздуха последний находится в аэростатическом равновесии как целое. Аэростатическое равновесие влажного воздуха является одним из основных фундаментов всех моделей атмосферной циркуляции. Распределение плотности воздуха по высоте в условиях аэростатического равновесия определяется высотой h = RT/Mg (с. 2634, ур. (8)) равномерно плотной атмосферы, которая зависит от температуры земной поверхности (с. 2634, строки 10-11). Так как среднегодовая температура земной поверхности уменьшается от экватора к полюсам, то распределение воздуха по высоте в аэростатическом равновесии изменяется. Это приводит к возникновению горизонтального градиента давления dp/dx, который ответственен за горизонтальные перемещения воздуха. Относительная величина этого градиента, (1/p)(dp/dx), совпадает по порядку величины с относительной величиной горизонтального градиента температуры (1/T)(dT/dx). Последняя величина имеет порядок 10-3 (100 км)-1. Это приводит к оценке dp/dx ~ p ´ 10-3 (100 км)-1 ~ 1 мбар (100 км)-1, что хорошо согласуется с наблюдениями. Ввиду вышесказанного, я привыкла считать, что и вертикальные, и горизонтальные движения воздушных масс имеют последовательное объяснение в метеорологии. Если авторы предлагают альтернативную или модифицированную картину, они бы, с моей точки зрения, существенно повысили убедительность своих результатов (возможно, в следующей статье), если бы четко и подробно обсудили, как их новый подход соотносится с традиционными и хорошо известными положениями метеорологии, которые я попыталась описать выше. Хочу также добавить, что я бы поддержала утверждение авторов, сделанное ими в ответе на комментарий Д-ра Савение, а именно, что интригующие закономерности распределения осадков, описанные авторами, имеют самостоятельную научную ценность, не зависящую от предложенного физического принципа (сила испарения). Я благодарю Н. Пахомову, чья любезная помощь с английским переводом позволила мне принять участие в этой интересной дискуссии. |
1. Вертикальные движения воздуха 1.1. Сила испарения и динамические и диффузионные потоки явного и скрытого тепла Сила испарения поднимает воздушные массы со скоростью w на
характерную высоту
Динамический поток скрытого тепла с земной поверхности в атмосферу,
вызываемый силой испарения, равен
Aw = w Эта теоретическая оценка, полученная из рассмотрения силы испарения, заставляющей воздух двигаться вертикально со скоростью w, находится в хорошем согласии с наблюдениями (напр., Palmen, Newton, 1969). Более того, поскольку gs растет с увеличением температуры поверхности, формула (1) объясняет наблюдаемый рост среднего числа Бовина от экватора к полюсам (Palmen, Newton, 1969). У земной поверхности к динамическим восходящим потокам явного и скрытого
тепла добавляются явный поток турбулентной теплопроводности
ac,
пропорциональный вертикальному градиенту температурры, и турбулентный
поток скрытого тепла aw, пропорциональный отклонению водяного пара от
аэростатического равновесия.
Оба потока возникают за счет атмосферной турбулентности.
Турбулентный поток явного тепла
ac выражается с помощью коэффициента
турбулентной диффузии (кинематической вязкости)
n как
ac = nCpNsGob. Полагая n = w Соотношение n = w В соответствии со вторым началом термодинамики как диффузионный, так и динамический потоки явного тепла направлены вверх, от теплых атмосферных слоев к холодным. Турбулентный поток атмосферного водяного пара также всегда направлен вверх в соответствии с неравновесным вертикальным распределением водяного пара. В то же время динамические потоки воздуха и водяного пара могут в общем случае быть направлены как вверх, так и вниз (области подъема и опускания воздушных масс). Поэтому в областях опускания восходящий диффузионный и нисходящий динамический потоки водяного пара у поверхности примерно совпадают по абсолютной величине и имеют противоположный знак. Это означает, что полный поток водяного пара в областях опускания, равный сумме динамического и диффузионного потоков, близок к нулю. Порядок величины этого потока не может быть оценен в рамках точности данного расмотрения. Можно лишь утверждать, что полный поток водяного пара у земной поверхности по абсолютной величине намного меньше динамического потока водяного пара. 1.2. Сила испарения и постоянный газовый состав сухого воздуха Как отмечено выше, сила испарения поднимает воздушные массы со скоростью w; это приводит к появлению динамического потока воздуха Fw = wN. Динамический поток каждого i-го газа воздушной смеси равен Fwi = wNi, где Ni -- молярная концентрация i-го газа. Внутри этого динамического потока, общего для всех газов, появляются турбулентные диффузионные потоки каждого газа. Эти потоки, как отмечалось в нашем ответе д-ру Шерману, пропорциональны отклонению градиентов концентраций газов воздуха от их значений в гидростатическом равновесии:
Первый член
С использованием значения bi для конкретных атмосферных газов получаем:
Турбулентные потоки (турбулентное перемешивание) атмосферных газов стремятся восстановить гидростатическое равновесие каждого газа, при котором разные газы имели бы разные вертикальные масштабы, а газовый состав сухого воздуха и его молекулярная масса менялись бы с высотой. Однако, как видно из (3), для всех газов их динамические потоки существенно превосходят турбулентные диффузионные. Поэтому можно заключить, что постоянный газовый состав сухого воздуха объясняется малой относительной величиной турбулентных потоков в сравнении с динамическими потоками каждого газа, поддерживаемыми силой испарения. Нужно отметить, что для CO2 при n = w
1.3. Выводы по вертикальным движениям воздуха В традиционном теоретическом рассмотрении конвективной неустойчивости, описанном д-ром Довгалюк, скорость w вертикальных движений воздуха и коэффициент тубрулентной диффузии атмосферного перемешивания остаются неопределенными; в моделировании они должны поэтому быть постулированы феноменологически. Разработанный же нами физический подход на основе силы испарения и неравновесного распределения атмосферного водяного пара позволяет количественно определить основные наблюдаемые параметры атмосферного транспорта явного и скрытого тепла (напр., отношение Бовина), а также параметры вертикального распределения и динамических потоков атмосферных газов. В частности, количественно объясняется наблюдаемое постоянство газового состава сухого воздуха, а также оценки среднеглобальной скорости вертикального движения воздушных масс и коэффициента турбулентной диффузии (кинематической вязкости) атмосферы. В нашей статье мы показываем, что сила испарения force возникает в условиях существования жидкой гидросферы и влажной почвы (важнейшее свойство земной поверхности). Сила испарения (и связанная с ней циркуляция воздуха) возникают, когда вертикальный отрицательный градиент температуры воздуха превосходит 1.2 К км-1 (с. 2635, строки 13, 19). Эта величина значительно меньше влажного адиабатического градиента 6 К км-1, который является критическим параметром в традиционном рассмотрении конвекции. Поэтому при наблюдаемом вертикальном отрицательном градиенте температуры воздуха, равном 6.5 К км-1, логические связное описание метеорологических явлений с необходимостью должно включать силу испарения. 2. Горизонтальные движения воздуха Когда водяной пар находится вне гидростатического равновесия и подвергается конденсации в атмосферной столбе, гидростатическое равновесие влажного воздуха как целого при существовании конденсации водяных паров в атмосфере невозможно. Такое равновесие противоречило бы закону Дальтона и кинетической теории газов, которая подтверждается всеми существующими в физике эмпирическими данными. При существовании конденсации водяных паров в атмосфере и силы испарения имеет место лишь аэростатическое равновесие сухого воздуха, смысл которого количественно описан нами в ответе на первый вопрос д-ра Шермана (сс. S1130-S1132). Поэтому далее в этом нашем ответе мы под аэростатическим равновесием будем подразумевать гидростатическое равновесие сухого воздуха. Действительно, как хорошо известно и отмечается д-ром Довгалюк, уменьшение температуры земной поверхности от экватора к полюсам зменяет распределение аэростатического равновесия воздуха. Масштаб высоты h (с. 2634, ур. (8)), являющийся основным параметром, характеризующим это распределение, изменяется прямо пропорционально температуре земной поверхности (с. 2634, строки 10,11). Это приводит к возникновению горизонтального градиента давления воздуха (барического градиента). Из уравнения состояния p = NRT имеем:
где x -- расстояние, отсчитываемое по меридиану, x = Rj , j -- долгота и R -- радиус Земли. Принимая, что средняя температура земной поверхности T ~ 300 К изменяется на ~30 К на расстоянии порядка ~104 км от экватора до полюсов и пренебрегая относительным изменением молярной плотности воздуха, можно заключить, что относительный градиент давления, равный относительному градиенту температуры, составляет около 10-5 км-1. Таким образом, при атмосферном давлении 103 бар, средний горизонтальный градиент давления действительно был бы порядка 1 bar (100 км)-1, что согласуется с наблюдениями. Однако такая оценка предполагает, что атмосферное давление на полюсах должно быть примерно на 10% меньше, чем на экваторе. Это противоречит наблюдениям: в среднем давление воздуха на уровне моря в приполярных областях примерно такое же или немного больше, чем в на экваторе. Это означает, что в производимой оценке барического градиента недопустимо опускать относительную величину градиента молярной плотности воздуха dN/(Ndx). С другой стороны, предполагая одинаковое атмосферное давление на экваторе и полюсах, легко показать, что максимум величины барического градиента, возникающего за счет разности температуры земной поверхности между экватором и полюсами, расположен на высоте порядка h (действительно, на земной поверхности мы положили барический градиент равным нулю, на больших высотах давление экспоненциально уменьшается, кроме h не существует других масштабов, определяющих распределение давления воздуха на высоте). На этих высотах турбулентная вязкость мала и, следовательно, перемешивание воздуха, выравнивающее температуру, должны были бы приводить к атмосферной циркуляции на достаточно больших высотах, практически не затрагивая земную поверхность на уровне моря, что противоречит наблюдениям. Упоминания проблем с традиционным рассмотрением общей циркуляции, базирующимся на уравнениях гидроаэродинамики (не учитывающих явно силу испарения) при использовании феноменологического коэффициента турбулентной вязкости нередки в литературе. Одной из таких проблем является, например, проблема неудовлетворительного теоретического описания циркуляции Хэдли (см., напр., Fang, Tung, 1999). Как показано в нашей работе, в традиционном метеорологическом подходе, не учитывающем силу испарения, нельзя объяснить существование лесного биотического насоса, продемонстрированное на основе эмпирических данных в нашей работе (см. раздел 2, сс. 2625-2633), отсутствие муссонного климата в пустынях (с. 2671, рис. 2) или экспоненциальное затухание осадков с проникновением океанской влаги в безлесные территории (сс. 2625-2628; 2671; рис. 2). Рассмотрение силы испарения показывает, что циркуляция Хэдли (пассаты) может существовать даже при нулевом градиенте температуры поверхности океана в тропической зоне. Наш подход также дает возможность получить теоретические оценки скоростей ветра в таких атмосферных структурах как ураганы и смерчи (см с. 2641 и ответ д-ру Шерману). В последние несколько десятилетий предприняты многочисленные попытки описания наблюдаемой циркуляции атмосферы с помощью множества глобальноциркуляционных моделей. Эти модели включают уравнения гидродинамики со всеми известными силами (Кориолиса, центробежной, трения (McGuffie and Henderson-Sellers, 2001), но сила испарения учтена до сих пор не была. Литература Fang, M. and Tung, K. K.: Time-dependent nonlinear Hadley circulation, J. Atmos. Sci., 56, 1797-1807, 1999. McGuffie, K. and Henderson-Sellers, A.: Forty years of numerical climate modelling, Int. J. Climatology, 21, 1067-1109, 2001. Palmen, E. and Newton, C. W.: Atmospheric circulation systems, their structure and physical interpretation, Academic Press, New York and London, 1969. |
|
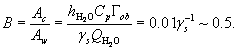 (1)
(1)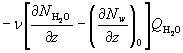 ,
где нижний индекс 0 указывает концентрацию
водяного пара, находящуюся в аэростатическом равновесии.
Используя
уравнение состояния для водяного пара
,
где нижний индекс 0 указывает концентрацию
водяного пара, находящуюся в аэростатическом равновесии.
Используя
уравнение состояния для водяного пара
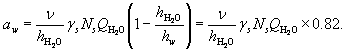 Полагая n = w
Полагая n = w