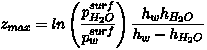Introduction

Main publication
(abstract)

Overview of the results

Comments and responses
[you are here]
List [1] [2] [3] [4] [5] [6] [7] [8] [9] [10]

De Melo Jorge Barbosa H. (2006) Interactive comment on "Biotic pump of atmospheric moisture as driver of the hydrological cycle on land" by A. M. Makarieva and V. G. Gorshkov. Hydrology and Earth System Sciences Discussions, 3, S1418-S1424. www.cosis.net/copernicus/EGU/hessd/3/S1418/hessd-3-S1418.pdf
The comment discusses the main biotic pump publication.
Informal title of the comment:
Physical concepts in section 3.1

Makarieva A.M., Gorshkov V.G. (2006) Interactive comment on "Biotic pump of atmospheric moisture as driver of the hydrological cycle on land" by A. M. Makarieva and V. G. Gorshkov. Hydrology and Earth System Sciences Discussions, 3, S1449-S1458. www.cosis.net/copernicus/EGU/hessd/3/S1449/hessd-3-S1449.pdf

In response to the comments of H. de Melo Jorge Barbosa:

Note: the original order of comments of Dr. H. de Melo Jorge Barbosa was changed to match the order of our responses. Consult the corresponding PDF for the original text.

As a physicist who have just recently changed field from astrophysics to meteorology I must say that I read this paper with great interest. It goes into the details of the physical meaning of meteorological concepts.

However, I do have some concerns about some of the physical and meteorological arguments used by the authors which I would like discuss. For the time being, I will only discuss section 3.1, where most of the concepts are. I will enumerate my comments with the corresponding page and line number.

P2638 l5

Quoting: "It equally acts on air volumes with positive and negative buoyancy,..."

You started the section 3 saying that air meant dry air... so if there is no water vapor, there should be no such force, right?

After that you say: "Quantitative consideration of this force, which creates upwelling air and water vapor fluxes (...)

Why should this "force" act on dry air? If "dry air" molecules are in a state of hydrostatic balance they should not move... If only water vapor is out of equilibrium, only the H₂O molecules should diffuse upwards trying to bring the vertical profile to equilibrium. And this would happen for all lapse rates between ~ 1.2km and 6 ~ 9.8 km which is quite a wide range (and therefore an important effect). In fact, you start section 3.2 citing Landau and Lifschitz about this subject. Could you give a more precise citation (chapter and page number) for equation 14?

Dr. de Melo Jorge Barbosa raises a number of questions that we now address in the order of what we envisage as their physical importance, with more fundamental issues discussed first.

Comment to P3638, L5 (p. S1423) questions the existence of the evaporative force, which constitutes the basis of the physical mechanism of the biotic pump that we proposed. The comment says (quote): "If "dry air" molecules are in a state of hydrostatic balance, they should not move... If only water vapor is out of equilibrium, only the H₂O molecules should diffuse upwards trying to bring the vertical profile to equilibrium."

These statements contradict the bases of the kinetic theory of gases. Gas is a physical state where molecules are at large distances from one another as compared to the radius of molecular interaction. The state of gas is determined by the spatial distribution of molecules and by the velocity distribution of molecules that is formed in the course of molecular collisions. At low gas densities, as those in the terrestrial atmosphere, the ideal gas approximation is valid. Pressure of ideal gas does not depend on the properties of molecules (their mass, atomic structure, scattering length etc.) but is exclusively determined by temperature T and molar density N, p = NRT, that is, on temperature and the total number of gas molecules of whatever nature.

Therefore, when molar density of a gas mixture deviates from equilibrium in a certain spatial area, local pressure of the gas mixture deviates from equilibrium as well. This leads to the appearance of a force acting on a unit volume of the gas mixture. This force is equal to the difference between the equilibrium pressure gradient and the existing (non-equilibrium) pressure gradient of the gas mixture. This process does not depend on whether the considered gaseous state is represented by only one gas or a mixture of several different gases. In the view of p = NRT, it does not matter whether molar density N deviates from equilibrium due to the change of molar densities of all mixture constituents or due to the change of the molar density of only one of them. Thus, when the molar density of water vapor deviates from equilibrium, this leads to the appearance of the evaporative force acting on the gas mixture as a whole, i.e. on the unit volume of moist air.

Illustration to our response (to the right)   (1) Black and white dots denote molecules of different gases. All gases in both compartments of the jar have equilibrium (equal) concentrations and partial pressures.   (2) One gas (white dots) is partially removed from the left compartment. When the partition is removed, the gas mixture from the right compartment moves dynamically to the left to compensate for the pressure shortage. (3) In the case of equilibrium pressures of different gases in the two compartments, removal of the partition initiates a diffusional flux of black molecules to the left, and of white molecules to the right, with no dynanic movements (motions) of gases as a whole.

 

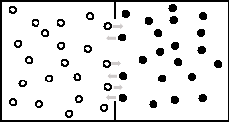
The same effect can be illustrated by the following simple example. Let us take a closed jar divided into two compartments by a gas-impermeable partition and fill both compartments with atmospheric air. In the initial state molar densities and partial pressures of all gases are equal in both compartments; gases in the two compartments are in equilibrium. Let us now partially remove some gaseous component (e.g., oxygen) from the first compartment. This can be done, for example, by initiating a chemical reaction turning oxygen into some non-gaseous oxygen-containing chemical substances (e.g., solid oxides). Partial pressure of oxygen in the first compartment will drop. However, as far as the total pressure of gas mixture is equal to the sum of partial pressures of all its constituents, total air pressure in the first compartment will drop as well as compared to air pressure in the second, intact compartment. When we now remove the partition, acted upon by the force equal to the appeared pressure gradient, all gases from the second compartment (and not only oxygen!) will move to the first compartment to compensate for the oxygen and total pressure shortage there.

Note that if we fill the first compartment in the jar with one gas, and the second compartment with a different gas, both gases having equal temperature and molar densities (and, hence, pressures), then, after removing the partition, a diffusion process will start mixing the gases and equating their molar densities in both compartments. There will be a diffusional flux of molecules of gas No. 1 to the second compartment, and of gas No. 2 -- to the first compartment. No pressure gradient, no force and no mass movements of gases will originate. In contrast, the process of equating non-equilibrium pressures of the gas mixture in the two compartments in the previous example is not a diffusion process, it is a dynamic mass movement of the gas mixture as a whole.

On a related note, it is several times mentioned in the comments that the non-equilibrium distribution of water vapor induces "upward motion" of water vapor (see comment to P2636, L7, p. S1422), while in the considered comment to P3638, L5 it is said that the non-equilibrium distribution of water vapor will make water vapor "diffuse" to the upper atmosphere. We thus believe it is appropriate to emphasize the distinction between motion of gas as a whole (which may only occur under the action of some force) and the thermal chaotic motion of air molecules. The latter is the driver of molecular diffusion and occurs irrespective of whether a force is acting on the gas or not. In atmospheric physics the word "motion" (vertical motion, upward motion etc.) is conventionally applied to denote dynamic mass movements of air (i.e. motion of air as a whole). In this sense there cannot be any dynamic motions of water vapor in the otherwise motionless atmosphere, but only motions of moist air as a whole.

To summarize, when the dry air constituents are in hydrostatic equilibrium, while water vapor is not, there is an upward-directed evaporative force acting on a unit volume of the entire gas mixture, moist air = dry air + water vapor. This force creates mass movement (or a dynamic (not diffusional) flux, as we referred to this movement in our response to Dr. Dovgaluk) of moist air in the atmosphere.

As requested in the comment to P3638, L5, we now clarify how expression (14) (p. 2638) for the evaporative force acting on moist air is obtained from the Euler equation of the hydrodynamics. When there is a force f acting on a unit gas volume with mass density r, this volume starts to accelerate in accordance with Newton's law: r dw/dt = f, where w is velocity. The time derivative dw/dt describes the change of velocity of the unit air volume, which moves in space. Hence, in the case of vertical movement . In the stationary case and we have , or, as far as z is the only independent variable, . In the presence of the gravitational force, total force acting on unit gas volume is f = - dp/dz -rg (z increases upwards), so we have:

.       (C1)

We do not have the English text of Landau and Lifshitz (1987) at hand, but from our Russian edition we believe that equation (C1) can easily be located by its number, (2.4), in Section 2 "Euler equation" of Chapter 1 "Ideal liquid".

Writing this equation for moist air (low index m), p_m = p + , r _m = r + , and taking into account that r = MN and that in hydrostatic equilibrium for dry air - dp/dz = MNg = r g (Eq. 7, p. 2633), we can see that the dry air terms cancel in the right-hand part of Eq. (C1). The only terms that remain, - d/dz - g, pertain to water vapor. Now making elementary substitutions = (/M_w)RT and h_w = RT/(M_wg), one arrives at expression (14) for the evaporative force acting on moist air as a whole. See also our reply to S. Sherman, pp. S1130-S1132. Note also that, as we mentioned in our reply to S. Sherman (S. 1131, L20-21), the minus sign at the first term in the right-hand side of the first equality in Eq. (14) was lost by mistake.

Concluding this issue, if there is no water vapor in the atmosphere, the evaporative force is zero. However, the evaporative force acting in one local area (e.g., over the ocean) can make the water-poor air in other areas (e.g., deserts) move as well, as prescribed by the continuity equation that governs atmospheric circulation.

2) Saturation of surface air and atmospheric column
(comments to P2634, L14 on p. S1419 and to P2636, L7 on p. S1421)

P2634, L14 I don't think that immediately above the wet soil or open water the air is saturated of water vapor. If it was like that, no extra water would ever evaporate because the exchange of H₂O molecules between the soil and this first saturated layer would always be in equilibrium. In the atmosphere, turbulence keeps recycling the surface air so that it is (almost) never totaly saturated.

P2636, L7

The reasoning starting at line 7 is not clear enough.

For instance, how does a situation where G > appear? For G = the atmosphere is completely saturated, .i.e., the maximum possible amount of water vapor (given by the PV diagram) is present at any heigh z. Any extra water vapor, at any level, would immediately condensate, warming the column and reducing G.

Moreover, at line 11 you say that "excessive moister is precipitating", but at line 8 you said that p_w(z) = (z), so there is not excess of water.

Another question: why G > means the column is saturated? Think of the atmosphere over a desert region, there is no water vapor... Hence do you mean that G > is not possible?

Any given vertical profile of humidity must be such that 0 < p_vap(z) ≤p^sat_H2O(z), for all z. When G > , < h_w. If vapor at the surface is saturated, then any possible humidity profile will be out of hydrostatic equilibrium. However, if the surface is not saturated, the profile cannot be in equilibrium above height:

or

but the profile can be in equilibrium (but not necessarily) below this height.

In any of these two cases, there will be an upward motion of water vapor trying to restore the equilibrium, within the part of the atmospheric column which is out of equi-librium. Notice that this upward motion does not depend on the profile being that of saturation. Supose, for instance, a particular profile p₁ that starts at saturation at the surface:

This profile is not the saturation profile and since 0.5 * < < h_w , it is out of hydrostatic equilibrium and will induce vertical motions. However, there will not be precipitation.

Just trying to summarize: you based your argument on the fact that the surface is always saturated of water vapor and hence, G > , the full profile is out of balance. This will lead to an upward motion. Moreover, since the column is fully saturated and lower air is moister then upper air, there will be precipitation during this updraft.

The points that I (particularly) need some clarification in this argument are:

1) Is the surface always saturated? In line 20 of this page you say it is not.

2) Why the column should be fully saturated (and not like p₁(z))?

The condition G > leads to saturation of the entire atmospheric column if only water vapor is saturated at the surface. In the absence of horizontal air movements this condition is always fulfilled when the rate at which water vapor is removed from the surface layer by vertical updrafts is less than the rate at which it is added to the surface layer in the course of evaporation. It is easy to show that at the considered vertical velocities of the order of 10^-3 m s^-1 this is always the case.

3) Specific issues

P2633, L20 Atmospheric air is not always in hydrostatic equilibrium (although it is always trying to be), and probably you don't think that it is. Better to have this paragraph rephrased.

Comment to P2633, L20, p. S1419
The first phrase of this paragraph can be changed to: "Hydrostatic equilibrium of dry air represents the basis of theoretical considerations of atmospheric processes".

P2634, L8 An isothermal atmosphere is not a good approximation, only the constant molar mass is... And only so because of the atmospheric circulation and turbulence which keeps the atmosphere mixed (Feynman), and there is no large sources or sinks of N₂ or O₂.

P2634, Eq. 9 - You should mention that in deriving eq (9) two assumption are made: V_liq << V_gas (good) and = cte, i.e., temperature independent (bad). However, since enthalpy of both liquid and vapor change with temperature, the difference between them, i.e. the enthalpy of vaporization is also temperature dependent. Temperature dependence of enthalpy can be estimated based on heat capacity, C_p , which, for simplicity can be taken as a constant. Then one can write:

(T₂) = (T₁) + DC_p(T₂-T₁)

A more sophisticated expression is found in Bruining et al (2003):

(T) = (7.1845e12 + 1.10486e10 * T - 8.8405e7 * T² + 1.6256e5 * T³ - 121.377 * T⁴)^1/2

where T is temperature in K, is in J/Kg. Rearranging the terms and writing in ^oC instead of K, one can approximate this expression by a linear equation:

This represents a decrease of 1000J/mol for every 25 o C increase in temperature. If you believe this linear dependence is weak enough that you can neglect it, you should give the arguments for that.

P2634, eq10 On the other hand, maybe you should avoid writing the approximate equation (9) at all. Instead, use directly the differential (and exact) form of the Clausius-Clapeyron equation

and equation (10) follows immediately.

Comments to P2634, Eq. 9, p. S1419 and P2634, Eq. 10, p. S1420
For a change of temperature from 0 to 100 ° C the value of changes by only 10%. In the temperature interval of interest, from z = 0 to it changes by a magnitude of the order of 1%. Constancy of is therefore a very good approximation for our analysis. It is mentioned in the comment that the exact Eq. (10) can be derived directly from the differential form of the Clausius-Clapeyron equation, which is valid for any dependence of on T; we agree. However, we do not think that such a change in our derivations would be appropriate, because formula (9) obtained by integrating the differential Clausius-Clapeyron equation at constant is similar in its form to the fundamental Boltzmann's distribution, is well-known and widely used in atmospheric analyses.

P2635, L14 I don't understand why do you need the approximation exp(-z/H) » 1 when deriving (11) from h_w = .

Comment to P2635, L14, p. S1420
The exact equation (11) obtained from formulae (8) and (10) has the form Hence, we have T = T_sexp(-z/H) and, consequently, dT/dz = (dT/dz)_s exp(-z/H) = exp(-z/H). The exponent exp(-z/H) » 1 is omitted in Eq. (11), as is stated in the text.

P2635, last paragraph.
First you described the situation G = as corresponding to a fully saturated atmosphere in hydrostatic equilibrium. In this paragraph you say that, for G < , there is only a superficial saturated layer and that the water is also in hydrostatic equilibrium. If the first layer is saturated in both cases, it will have the same partial pressure of H₂O in both cases (assuming the same surface temperature). Hence, since for the second case there is less water vapor in the atmosphere, the column should not be in equilibrium (for the water vapor). There should be a tendency to expand the column and distribute the total column water vapor in a vertical profile that is in equilibrium. In such a situation, the surface air would always be drying out (losing water to the upper levels by diffusion or turbulent fluxes) while at the same time, water from the surface should be evaporating. Therefore, there should be fluxes of water vapor into the atmosphere (at least enough to keep the diffusion process).

Comment to P2635, last paragraph, p. S1420
The reasoning in the comment is based on the incorrect premise that the amount of water vapor in the unsaturated atmosperic column at G < is less than the amount of water vapor in the fully saturated atmospheric column at G = at equal surface temperatures. In reality, the amount of water vapor in the column at G < is larger than at G = , as far as pressure drops more slowly when the temperature lapse rate is smaller, see formula (8) and our response to comment P2634, L8, p. S2429 above.

The general point that is overlooked in the comment is that in the first case of temperature dropping only slowly with height, G < , the atmosphere is on average warmer than in the second case when, due to the more rapid decrease of temperature with height, it is on average colder. The saturated amount of water vapor at low temperature is not necessarily higher than the unsaturated amount of water vapor at a higher temperature. Therefore, the conclusions about the non-equilibrium state of water vapor and existence of upward fluxes of water vapor at G < do not hold.

P2636, L1
It is not the same molecules that evaporated into air that immediately condense. The equilibrium is maintained because air and surface exchange the same amount of water molecules, which are carrying (on average) the same energy, but these are not (necessarily) the same molecules.

Comment to P2636, L1, p. S1421
We do not state anywhere in the paper that it is the same molecules that evaporate into the atmosphere that immediately condense.

P2637, L21
Quoting: "After averaging over a horizontal scale exceeding the characteristic height h of the atmosphere, mean Archimedes force turns to zero. This means that the total air volume above an area greatly exceeding h² cannot be caused to move anywhere by the Archimedes force."

This assertion is not obvious at all and you should give a proof of that. In fact, consider a mesoscale convective complex. These systems which extend over large areas (typical size 100km x 100km) show strong updrafts associated with intense convection of buoyant parcels. Isn't this a counter example?

Comment to 2631, L21, p. S1422

Our statement that the Archimedes force cannot drive atmospheric motions over areas exceeding h² is based on the physically transparent fact that h is the only relevant vertical length scale of the atmosphere. In our paper we show how the evaporative force can drive large-scale atmospheric circulation. We do not base our consideration on the Archimedes force and, hence, we do not need to prove this statement. This statement would need to be disproved in an attempt to show that the Archimedes force is able to drive large-scale atmospheric motions. The example of the observed extensive updraft regions in the real atmosphere is not a counter-example to our statement. We have shown (p. 2641, L3-19) that the evaporative force can lead to strong updrafts with vertical velocities of up to several dozens m s^-1.

REFERENCES
Feymman: "The Feymman Lectures on Physics", chapter 40-1
Bruining, 2003: J. BRUINING et al., "Steam injection into water-saturated porous rock", Computational and Applied Mathematics, Vol. 22, N. 3, pp. 359-395

Held, I.M. and Soden, B.J.: Water vapor feedback and global warming, Annu. Rev. Energy Environ. 25, 441-475, 2000.

Feynman, R. P., Leighton, R. B. and Sands, M.: The Feynman lectures on physics, Vol. 1.4. Chapter 42, Section 1. Addison-Wesley Publishing Company, Reading, 1963.