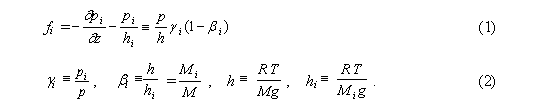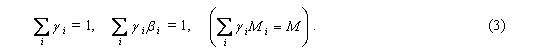Introduction

Main publication
(abstract)

Overview of the results

Comments and responses
[you are here]
List [1] [2] [3] [4] [5] [6] [7] [8] [9] [10]

Sherman S. (2006) Interactive comment on "Biotic pump of atmospheric moisture as driver of the hydrological cycle on land" by A. M. Makarieva and V. G. Gorshkov. Hydrology and Earth System Sciences Discussions, 3, S1124-S1126. www.cosis.net/copernicus/EGU/hessd/3/S1124/hessd-3-S1124.pdf
The comment discusses the main biotic pump publication.
Informal title of the comment:
Comment on the evaporative force

I would like to comment and actually have two questions on the physical mechanism of the biotic pump proposed by the authors.

From the physicist's perspective I am convinced by the authors' reasoning that atmospheric water vapor cannot be in hydrostatic equilibrium above the open water surface or moist soil surface if the vertical temperature lapse rate G exceeds the threshold value = 1.2 K km^-1 (p. 2636, eq. (13)), as is the case in the Earth's atmosphere. (I find it remarkable that, to my knowledge, this apparently important phenomenon is never mentioned in the basic physical texts where atmospheric gases are discussed. One can always read about such things as convective instability and adiabatic lapse rate G_a (e.g., Landau, LD, Lifshitz, EM, Course of Theoretical Physics, Volume 6, Fluid Mechanics), but nothing about the non-equilibrium water vapor and .)

So at G > water vapor is saturated and cannot be in hydrostatic equilibrium - when water vapor pressure at any height is balanced by the weight of the water vapor above that height. This is obvious if one considers water vapor alone or a hypothetical case of an atmosphere consisting of water vapor only. Indeed, water vapor concentration cannot exceed the saturated one. Saturated concentration exponentially diminishes with decreasing temperature in accordance with the physical law of Clapeyron-Clausius. When temperature is dropping with height sufficiently quickly, less and less water vapor can be present at a given height. So starting from some threshold lapse rate the total weight of water vapor in the atmospheric column above a given height becomes less than local vapor pressure. This leads to the origin of an upward-directed force termed ''evaporative force" by the authors. In my view, this term is indeed justified for the terrestrial conditions which correspond to the existence of liquid hydrosphere (open water surface of the oceans and moist soil surface), where water vapor is always saturated immediately near the surface. In this case evaporation of moisture from the Earth's surface compensates precipitation of condensed liquid water back to the surface. The power of evaporation must be maintained by solar energy.

In reality water vapor is mixed with other air constituents. Consider moist air, which is originally in hydrostatic equilibrium, where water vapor starts to condense somewhere in the atmospheric column and is leaving the atmosphere in the form of precipitation. In such a case in that volume where moisture condensed and which, prior to condensation, was in hydrostatic equilibrium, the atmospheric air becomes rarified and its pressure drops. As far as I understand, the appearing surplus of the vertical air pressure gradient, uncompensated by the weight of atmospheric column, creates the evaporative force. This force drives moist air into that area, i.e. it leads to formation of atmospheric circulation, as described by the authors.

(1) However, it remains unclear what does hydrostatic equilibrium mean when applied to the real moist air. It is well-known that the equilibrium Boltzmann's distribution for individual gases with different molar masses should be manifested as different scale heights for the vertical distributions of the gases. So in equilibrium concentration of each gas drops exponentially with height with each its own e-folding length determined by its molar mass. This does not conform with the observations - the relative ratio of different air constituents practically does not change with height in the troposphere, as noted also by the authors (p. 2534). I think it would be productive if the authors explained in greater details how the vertical constancy of relative concentration of air constituents (constant ''mixing ratio" in the meteorological literature) enters the new picture that they propose.

(2) The second concern is that when moisture undergoes condensation at a given height, it, as far as I understand, mostly produces cloudiness which remains in the atmosphere and does not precipitate. The weight of this cloudiness is - obviously - exactly equal to the weight of the water vapor that condensed and left the gaseous phase. The gravitational pressure exerted by cloudiness on the atmospheric column below could possibly compensate the excessive water vapor pressure that appears due to the non-equilibrium state of atmospheric water vapor. In other words, will the evaporative force still form and the fluxes of moist air arise in the case of cloud formation in the absence of precipitation?

Makarieva A.M., Gorshkov V.G. (2006) Interactive comment on "Biotic pump of atmospheric moisture as driver of the hydrological cycle on land" by A. M. Makarieva and V. G. Gorshkov. Hydrology and Earth System Sciences Discussions, 3, S1130-S1134. www.cosis.net/copernicus/EGU/hessd/3/S1130/hessd-3-S1130.pdf

In response to the two physical questions posed by S. Sherman:

1. Hydrostatic equilibrium and constant mixing ratio of atmospheric gases. According to Dalton's law, hydrostatic equilibrium must independently hold for all partial pressures of all air constituents. This follows from the kinetic theory of gases. Kinetic theory describes hydrostatic equilibrium as the state when fluxes of molecules of each gas via any plane (horizontal, in the considered case) in both directions, i.e. up and down, are equal to each other. In this state each gas obeys Boltzmann's distribution (Feynmann et al., 1963). As far as molar masses of dry air constituents are all different, the hydrostatic equilibrium should correspond, as pointed out in the comment, to different scale heights of the vertical distribution of different air gases.

The observed constancy of the mixing ratio of dry air constituents in the troposphere, i.e. a single scale height for all gases, means that each of these gases is out of equilibrium. Process when the initially non-equilibrium partial pressure changes towards equilibrium in a gas mixture or liquid solution is the basis of osmosis. For each i-th air gas one can formally introduce the osmotic force f_i equal to the difference of the partial pressure gradient taken with the opposite sign, on the one hand, and weight of the column of this gas above the considered height, on the other:

Here M_i and M, h_i and h, p_i and p are molar masses, scale heights and (partial) pressures of the i-th gas and air as a whole, respectively; g_i is the mixing ratio of the i-th gas (i.e. its relative contribution into total air pressure: p_ipi = N_iRT, p = NRT, g_i = N_i/N, where N_i and N are molar densities of the i-th gas and air as a whole, respectively). Taking into account that, according to observations, the gaseous composition and, hence, molar mass of dry air is height-independent, we obtain the following two sum rules:

Expression (1) for the osmotic force f_i has the same form as the expression for the evaporative force of the water vapor (p. 2638, Eq. (14), note that the minus sign at the term dp_H2O/dz in Eq. (14) was lost by mistake).

It is easy to demonstrate numerically that even for the main atmospheric gases N₂ and O₂ their osmotic forces f_i (1) are several times smaller than the evaporative force of the water vapor, because the value of b_i (2) for these gases is close to unity. It is worthy noting, however, that the osmotic forces for N₂ and O₂ are opposite in sign. As far as b_O2 > 1, the equilibrium Boltzmann's distribution of oxygen would be compressed as compared to the observed vertical air distribution (same as water vapor), while equilibrium nitrogen would be "stretched" as compared to air due to b_N2 < 1. The cumulative osmotic force acting on dry air appears to be equal to zero as governed by the above sum rules (3):

Thus, remarkably, from the observed constancy of M it can be derived that dry air as a whole is in hydrostatic equilibrium (4). However, water vapor is not in hydrostatic equilibrium. Therefore moist air as a whole is out of hydrostatic equilibrium as well: each unit volume of moist air is acted upon by the evaporative force conditioned by the non-equilibrium state of atmospheric water vapor.

2. We now discuss the existence of the evaporative force in the presence of cloudiness.

When water vapor undergoes condensation, molar volume of H₂O (i.e. volume occupied by one mole of H₂O) decreases by thousands of times. Partial pressure of water vapor decreases by the same amount and can be neglected. This process corresponds to disappearance ("annihilation") of water vapor from the considered air volume. Thus, even if there is no precipitation and water droplets remain in the air as cloudiness, total pressure of moist air in the region of condensation diminishes. There appears the evaporative force generating air circulation as described in the paper. Moreover, it is namely the evaporative force that in the stationary case supports cloudiness at a particular height in the troposphere. When cloudiness is strong (much liquid water in the atmospheric column) and covers extensive areas of linear size greatly exceeding height of the tropospere, it can almost completely absorb the vertical impulse imparted to it by the evaporative force, so that practically no horizontal fluxes of air will be formed. Such cloudiness can hang practically motionless or move very slowly.

Formation of patchy cloudiness like stormy clouds is, on the other hand, always accompanied by horizontal winds, as described in the paper. The larger the scale height of the condensation process, the larger the vertical path along which the evaporative force is acting accelerating the air, the higher the final vertical and horizontal velocities that the accelerating air masses ultimately acquire. Hurricanes and tornadoes, as also mentioned in the paper, arise when the condensation process in a local horizontal area spreads to the maximum height in the atmosphere (p. 2641, line 9). There appears a horizontal influx of air into this area, so the local high value of the evaporative force is maintained by the horizontal input of gaseous moisture that evaporated in the neighboring areas. This further enhances moisture condensation in the considered area so that the evaporative force and, consequently, wind speed grow even further. When all water vapor in the region occupied by the tornado (or hurricane) is condensed, the tornado can persist if only it rapidly moves to other areas with large stores of water vapor. The higher tornado wind velocity, the more rapidly the tornado must move to persist (Gorshkov, 1995).

Total power of hurricanes and tornadoes is limited by solar energy that, over a long time, was spent on evaporation of water in the large area along the path of these wind structures. However, the release of latent heat in the course of vapor condensation within the hurricane does not lead to formation of ordered dynamic processes (winds). Energy is transformed in the following order: solar energy leads to water evaporation; water vapor generates the evaporative force which accelerates air masses and creates hurricanes and tornadoes; the dynamic energy of moving air masses undergoes dissipation and heats the air. Most part of energy spent on evaporation is ultimately released in the form of latent heat after condensation of water vapor. Thermal energy of heated air is, with help of greenhouse gases, converted to thermal radiation that leaves into space (pp. 2660, 2661).

References

Feynman, R. P., Leighton, R. B. and Sands, M.: The Feynman lectures on physics, Vol. 1, Addison-Wesley Publishing Company, Reading, 1963.

Gorshkov, V. G.: Physical and biological bases of life stability, Springer, Berlin, 1995.