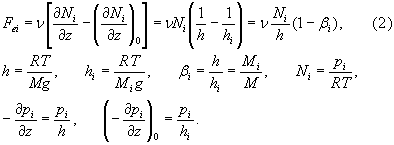You are on the first web site of Biotic Regulation. Since February 14, 2008 it is no longer updated. Welcome to www.bioticregulation.ru! |
Hot topic: Biotic pump of atmospheric moisture
|
Comments and responses |
Comment
Dovgaluk Y. (2006) Interactive comment on "Biotic pump of atmospheric
moisture as driver of the hydrological cycle on land" by A. M. Makarieva
and V. G. Gorshkov. Hydrology and Earth System Sciences Discussions,
3, S1135-S1137.
www.cosis.net/copernicus/EGU/hessd/3/S1135/hessd-3-S1135.pdf
I have read the paper with great interest; the authors aim to build a coherent picture of atmospheric circulation based on the so-called evaporative force that they introduce. I confess I could not find any faults in their presentation. Still when I try to analyze the authors' propositions at the background of the conventional meteorological principles I feel somewhat puzzled. The authors do touch upon on how their new physical approach relates to some basic meteorological notions (pp. 2637-2638), but in my view this point deserves a much more detailed discussion. |
ResponseMakarieva A.M., Gorshkov V.G. (2006) Interactive comment on "Biotic pump of atmospheric moisture as driver of the hydrological cycle on land" by A. M. Makarieva and V. G. Gorshkov. Hydrology and Earth System Sciences Discussions, 3, S1176-S1184. www.cosis.net/copernicus/EGU/hessd/3/S1176/hessd-3-S1176.pdf In response to the comments of Y. Dovgaluk: Dr. Dovgaluk raises the question of how the notion of biotic pump and the underlying physics (evaporative force) relate to the widely accepted paradigms of the modern meteorological thought, namely (1) convective instability for vertical air movements and (2) temperature-related barometric gradient for horizontal air movements. In our response we first show that the proposed approach quantitatively accounts for the major observed parameters of atmospheric circulation and then discuss the advantages of this approach as well as the critical points in the traditional meteorological paradigm. | |
|
1. In meteorology fluxes of sensible heat are related to convective instability of air masses; this instability arises under conditions of the observed air temperature lapse rate Gob = 6.5 K km-1. If there occasionally appears an air parcel with positive buoyancy (i.e. more heated and less heavy than equal volumes of the surrounding atmosphere), this volume starts to rise acted upon by the Archimedes force. As is well-known, temperature of the adiabatically ascending air parcel decreases with height at a rate of 9.8 K km-1 (and about 6 K km-1 for moist air due to heat release after condensation of water vapor). Since the observed lapse rate 6.5 K km-1 is greater than the moist adiabatic lapse rate, the ascending air volume will always remain warmer and less heavy than the surrounding air and, since, will infinitely continue its movement. Similarly, air parcels of higher volume density (negative buoyancy) will infinitely move downward until they reach the Earth's surface. Ascent and descent of such air masses create atmospheric turbulence, which is responsible for the observed vertical fluxes of the sensible and latent heat. These fluxes uniformly mix the atmosphere, and this is why in the troposphere the mixing ratio of gases in dry air is uniform and height-independent. These very fluxes maintain clouds. 2. It is widely accepted in meteorology that under the condition of turbulent mixing of moist air, the latter is in hydrostatic equilibrium. Hydrostatic equilibrium of moist air is one of the fundamentals in all models of atmospheric circulation. Air density in hydrostatic equilibrium is determined by the scale height h = RT/Mg (p. 2634, eq. (8)), which, in its turn, depends on surface temperature (p. 2634, lines 10- 11). As far as the annual mean surface temperature decreases from equator to the poles, the vertical distribution of air masses changes with latitude as well. This leads to the appearance of the horizontal pressure gradient for atmospheric air, dp/dx, which drives horizontal air movements. Its relative magnitude, (1/p)(dp/dx), coincides by the order of magnitude with the relative magnitude of the latitudinal temperature gradient (1/T)(dT/dx). The latter is of the order of 10-3 (100 km)-1. This gives an estimate of dp/dx ~ p ´ 10-3 (100 km)-1 ~ 1 mbar (100 km)-1, and this agrees well with observations. In the view of the above I was used to think that both vertical and horizontal movements of air masses all have their consistent explanation in meteorology. If the authors propose an alternative or modified picture, they would, in my view, greatly enhance their impact (perhaps with a follow-up paper), if they explicitly discussed the edges at which their approach meets the conventional and well-known meteorological viewpoint that I have attempted to outline above. I also add that I would support the authors' claim which they made in response to the comment of Dr. Savenije, namely that the intriguing precipitation patterns that they report have a self-contained value independent of the proposed underlying physical principle (the evaporative force). Acknowledgement. I thank N. Pakhomova whose kind help with my English enabled me to participate in this interesting discussion. |
1. Vertical air movements 1.1. The evaporative force and the dynamic and diffusional fluxes of sensible and latent heat The evaporative force rises air masses at velocity w to the characteristic height The dynamic flux of latent heat from the surface to the vapor-saturated atmosphere, driven by the evaporative force, is equal to Aw = w This theoretical estimate obtained from the consideration of the evaporative force that makes air move vertically at a speed w agrees satisfactorily with observations (e.g., Palmen and Newton, 1969). Moreover, since gs grows with surface temperature, formula (1) theoretically explains the observed pattern when the mean Bowen ratio is lowest at the equator and grows towards the poles (Palmen and Newton, 1969). At the Earth's surface the dynamic fluxes of sensible and latent heat are supplemented by the diffusional flux ac of sensible heat, that is proportional to the vertical lapse rate of air temperature, and by the diffusional flux aw of latent heat dictated by the non-equilibrium state of atmospheric water vapor. Both fluxes arise due to atmospheric turbulence. Eddy flux of sensible heat ac is expressed via the coefficient of eddy diffusivity (kinematic viscosity) n as ac = nCpNsGob. Putting n = w Expression n = w In accordance with the second law of thermodynamics both diffusional and dynamic fluxes of sensible heat are directed upward, from the warmer to the colder atmospheric layers. Eddy flux of atmospheric water vapor is also always directed upward as dictated by the non-equilibrium vertical distribution of water vapor. In the meantime dynamic (mass) fluxes of air and atmospheric water vapor can, generally, be directed either up or down (upwelling and downwelling regions of the atmosphere). Thus, in the regions of downwelling the upward diffusional and the downward dynamic fluxes of water vapor approximately coincide in magnitude at the surface and are of opposite sign. This means that the total flux of water vapor in the regions of downwelling, which is equal to the sum of the dynamic and diffusional fluxes, is close to zero. The order of magnitude of this flux cannot be estimated within the accuracy of the above considerations, we can only predict that it is much less than the absolute magnitude of the dynamic flux of water vapor. 1.2. The evaporative force and constant mixing ratio of dry air As already noted, the evaporative force rises air masses at velocity w; this leads to formation of the dynamic air flux Fw = wN. Dynamic flux of each i-th gas in the air mixture is Fwi = wNi, where Ni is molar concentration of the i-th gas. Within this dynamic flow common for all gases there appear additional eddy diffusional fluxes of each gas. These fluxes, as we mentioned in our response to Dr. Sherman, are proportional to the deviation of the concentration gradients of air gases from their hydrostatic equilibrium values:
The first term
Using bi for air gases we obtain:
Eddy fluxes (turbulent mixing) of atmospheric gases work to restore the hydrostatic equilibrium of each gas, when different gases would have different scale heights and the mixing ratio of dry air and its molecular mass would be changing with height. However, as can be seen from (3), for all gases their dynamic fluxes are much greater than the eddy diffusional fluxes. Hence, it can be concluded that the constant mixing ratio of dry air can be explained by the small relative value of eddy fluxes as compared to the dynamic fluxes of each gas maintained by the evaporative force. It should be noted that for CO2 at n = w
1.3. Conclusions on vertical air movements In the traditional theoretical consideration of convective instability outlined by Dr. Dovgaluk the velocity w of the vertical air movements and the eddy diffusion coefficient for atmospheric mixing remain undetermined; for modelling purposes they have therefore to be postulated phenomenologically. In contrast, the developed physical approach based on the evaporative force and the non-equilibrium distribution of atmospheric water vapor allows one to quantify the major observed parameters of the atmospheric transport of sensible and latent heat (e.g., Bowen ratio), as well as of the vertical distribution and mass fluxes of air gases. In particular, it numerically explains the observed constancy of the mixing ratio of dry air and estimates the global mean vertical velocity of air movements and the eddy diffusion coefficient (kinematic viscosity) of the atmosphere. In our paper we demonstrate that the evaporative force exists in the presence of a liquid hydrosphere and moist soil surface (the inherent property of the planetary surface of Earth). The evaporative force (and the associated air circulation) arise when the vertical lapse rate of air temperature exceeds 1.2 K km-1 (p. 2635, lines 13, 19). This value is much less than the moist adiabatic lapse rate of 6 K km-1, which is a critical parameter in the conventional consideration of convection. Hence, at the observed vertical lapse rate of air temperature of 6.5 K km-1 a consistent theoretical description of meteorological phenomena should necessarily include the evaporative force. 2. Horizontal air movements When water vapor is out of hydrostatic equilibrium and undergoes condensation in the atmospheric column, hydrostatic equilibrium of moist air as a whole is impossible as contradicting the Dalton's law and the kinetic theory of gases, the latter supported by all existing empirical data. In the presence of the evaporative force it is only dry air as a whole that can be in hydrostatic equilibrium; we discussed the physical meaning of this equilibrium in our response to the comments of Dr. Sherman (pp. S1130-S1132). So below under hydrostatic equilibrium we understand hydrostatic equilibrium of dry air. Indeed, as is well-known and also pointed out by Dr. Dovgaluk, the decrease of surface temperature from the equator to the poles changes the hydrostatic equilibrium of atmospheric air. Scale height h (p. 2634, Eq. (8)), which describes the equilibrium distribution of air, changes proportionally to the surface temperature (p. 2634, lines 10-11). This creates horizontal gradient of air pressure (barometric gradient). From the equation of state p = NRT we have: where x is distance counted along the meridian, x = Rj , j is longitude and R is Earth's radius. Taking that mean surface temperature T ~ 300 K changes by ~30 K over the distance ~104 km from equator to the poles and neglecting the relative change of air molar density, one can conclude that the relative pressure gradient, equal to the relative temperature gradient, is around 10-5 km-1. Thus, at mean air pressure of 103 bar, mean horizontal gradient of air pressure would be indeed 1 bar (100 km)-1, which agrees with observations. However, such an estimate presumes that atmospheric pressure at the poles should be about 10% less than at the equator. This is not supported by observations -- atmospheric pressure at the poles is approximately the same or even slightly higher than at the equator. This means that it is inappropriate to neglect the relative gradient dN/(Ndx) of air molar density when estimating the horizontal gradient of air pressure. On the other hand, assuming equal atmospheric pressure at the equator and the poles it is easy to show that the horizontal barometric gradient related to the horizontal gradient of surface temperature is maximized at a height close to height h (indeed, the barometric gradient is put zero at the surface; air pressure exponentially declines with height; and there is no other height scale except h). At such heights the kinematic viscosity is low; consequently, air mixing working to equate air temperature could have led to atmospheric circulation in the upper atmospheric layers only, with little impact on the lower troposphere. Such pattern apparently contradicts the observations. Generally, problems with the conventional account for general circulation based on the equations of hydrodynamics where the kinematic viscosity is borrowed from observations, are not uncommon in the literature. For example, one of such problems is the problem of the unsatisfactory theoretical representation of Hadley circulation (e.g., Fang and Tung, 1999). As shown in our paper, the conventional meteorological approach cannot explain the existence of the biotic pump of atmospheric moisture that was demonstrated on the basis of precipitation data (see Section 2, pp. 2625-2633 in the paper). Neither can it account for the absence of a monsoon-like climate in deserts (p. 2671, Fig. 2) or for the exponential decline of precipitation with distance from the ocean in the non-forested areas (pp. 2625-2628; 2671; Fig. 2). Consideration of the evaporative force predicts that Hadley circulation (trade winds) can exist even at zero gradient of sea surface temperatures in the tropical zone. Our approach also yields theoretical estimates of wind speeds in such atmospheric structures as hurricanes and tornadoes (see p. 2641 and our response to Dr. Sherman). In the last several decades years many attempts have been made to describe the observed atmospheric circulation with use of various numerical general circulation models. These models incorporate the equations of hydrodynamics with all the known forces (Coriolis force, friction force, centripetal force) (McGuffie and Henderson-Sellers, 2001), but the evaporative force has been ignored. References Fang, M. and Tung, K. K.: Time-dependent nonlinear Hadley circulation, J. Atmos. Sci., 56, 1797-1807, 1999. McGuffie, K. and Henderson-Sellers, A.: Forty years of numerical climate modelling, Int. J. Climatology, 21, 1067-1109, 2001. Palmen, E. and Newton, C. W.: Atmospheric circulation systems, their structure and physical interpretation, Academic Press, New York and London, 1969. |
|
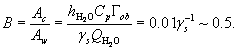 (1)
(1)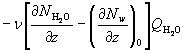 , where low index "0" refers to the concentration gradient of water vapor in hydrostatic equilibrium. Using the equation of state for water vapor,
, where low index "0" refers to the concentration gradient of water vapor in hydrostatic equilibrium. Using the equation of state for water vapor, 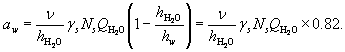 Putting n = w
Putting n = w